发布于 由editor

Liutex理论的数学基础

刘超群和俞一飞，美国德州大学阿灵顿分校，2023年4月10号
 
Liutex是涡的数学定义，是第三代涡识别方法的核心。本文介绍了Liutex理论的数学基础，包括矩阵运算与向量/张量运算的区别和速度张量的正确表达式。老的表达式用了Hamilton Del V代表速度梯度张量，虽然被数学和流体力学教科书广泛采用，但并不正确，这也许是人类为什么要化一百六十年才找到涡的正确表达式，也就是花了一百六十年才找到Liutex。 本文同时给出速度梯度张量的主表达式和主分解，推导了Q-和P-坐标旋转的公式。它们也是新流体运动学的关键。正确的速度梯度张量的散度公式也在本文给出，这可能对开发新的流体力学控制方程极为重要。图1显示对一个经典的Lamb-Oseen涡，只有Liutex显示最精确，用Q-判据和涡量显示涡都不准确。
 
                      
                                  （a）                                                        （b）
                                            
                                  （c）                                                        （d）
 
图1. Lamb-Oseen涡识别比较：(a)Q-判据 (b)涡量 (c) Liutex (d) Liutex 向量代表转轴方向；图中箭头代表流体速度方向
 
 
本期，我们推荐美国德州大学阿灵顿分校刘超群和俞一飞于近期在Journal of Hydrodynamics（第34卷第6期）发表的关于“Liutex理论的数学基础”的特色文章。
Mathematical foundation of Liutex theory,
 

编辑导读

 

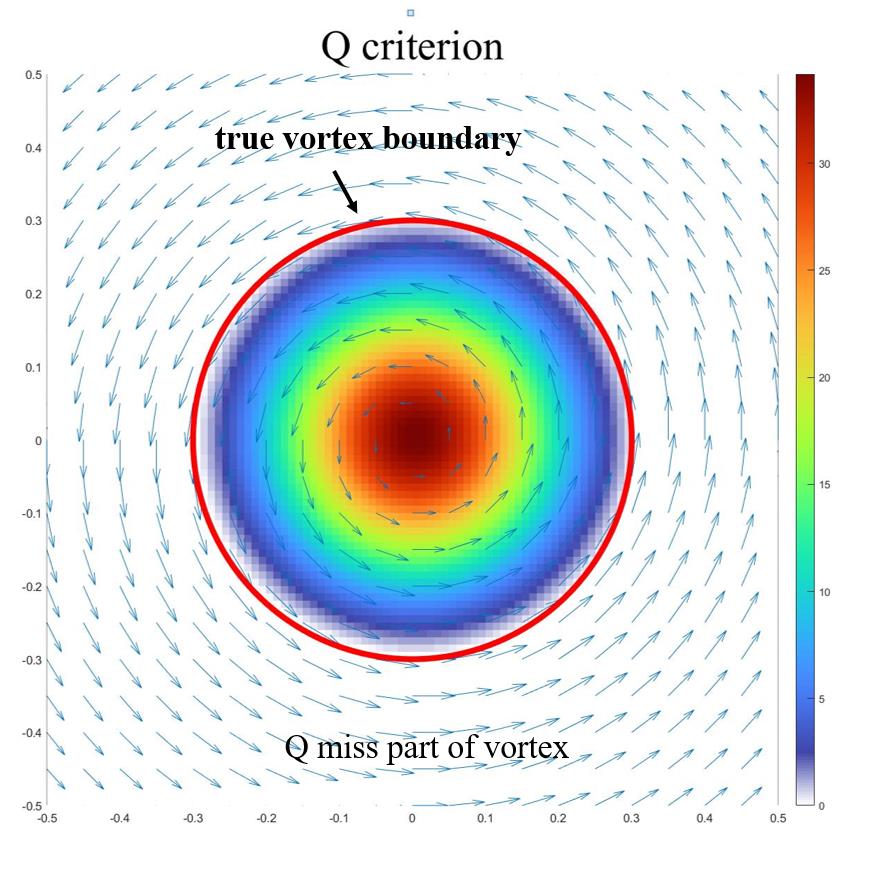
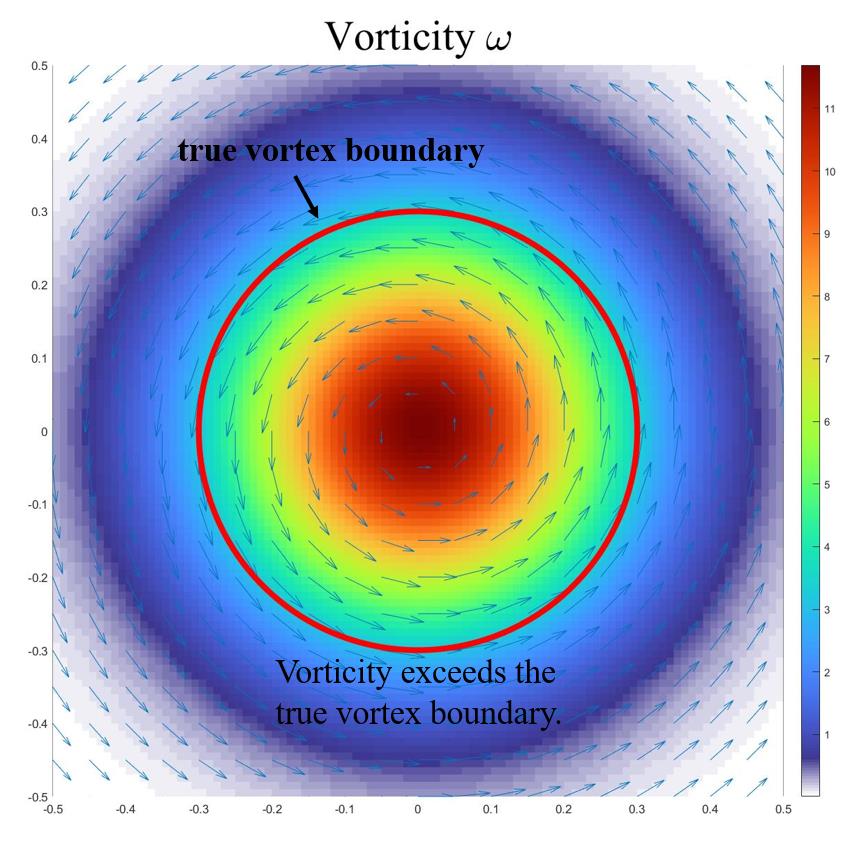
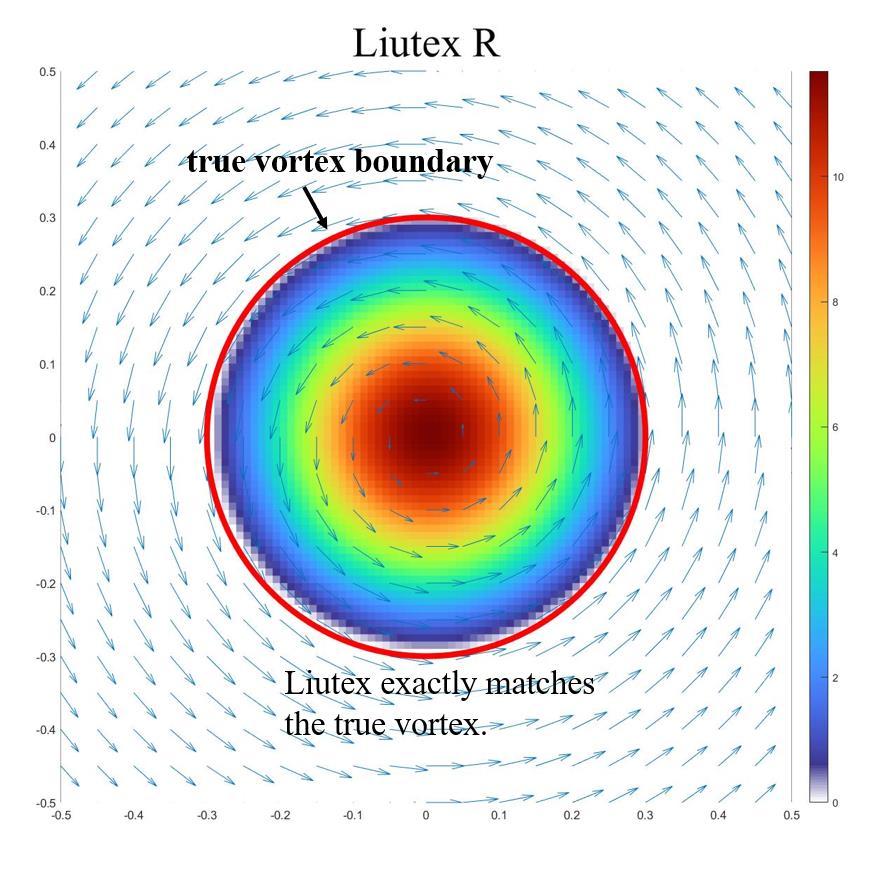
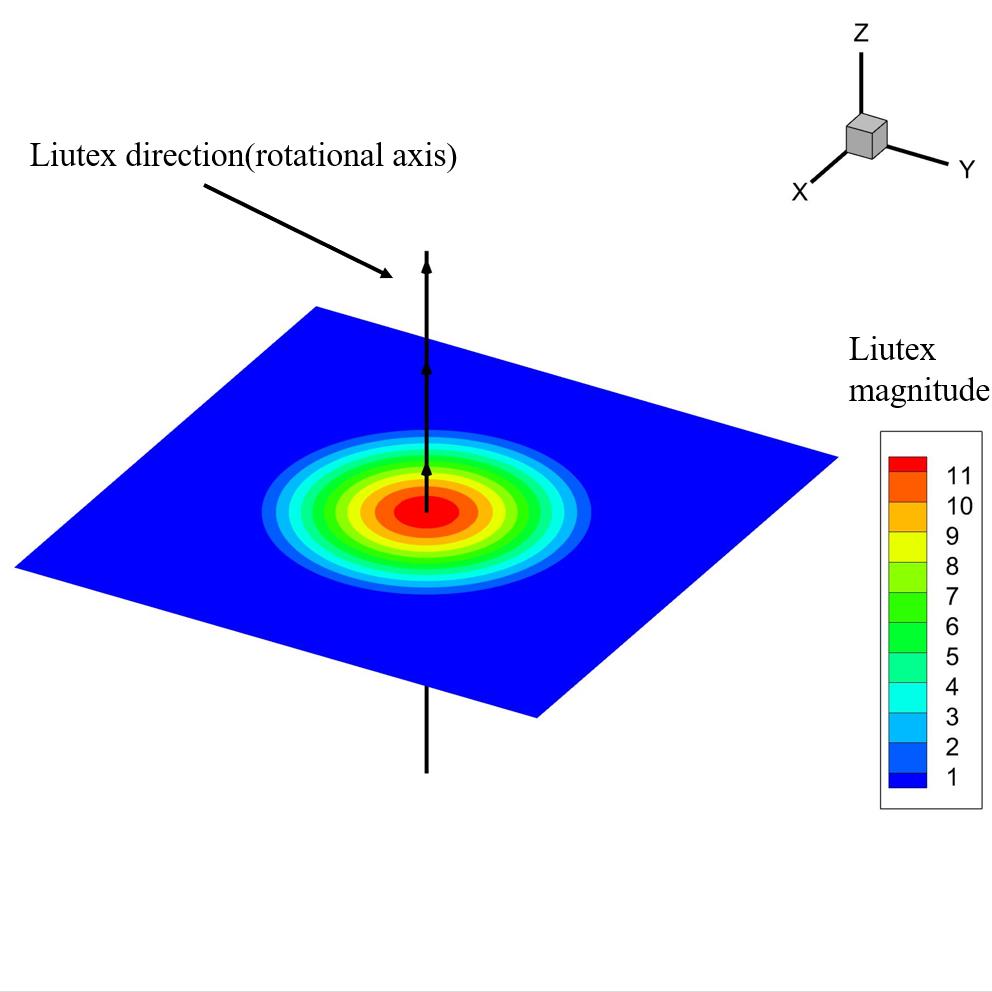
涡是流体转动，在宇宙无处不在，也是人类现在面临的重大问题，比如龙卷风，飓风，气候变化，心血管疾病，大气污染，湍流等等没有一个与涡无关。但是自古以来，直到2018年美国UTA（University of Texas at Arlington）刘超群团队在人类历史上首次给出涡的数学定义也就是Liutex之前（见PoF2018, JHD2019），涡始终没有明确的数学定义。赫姆霍兹1858年用涡丝也就是无限小的涡量管（Vorticity Tube）定义涡，我们称之为涡的第一代定义。尽管赫氏理论一百六十多年来为全世界学术界广泛接受，并写在几乎所有流体力学教科书上，比如Wu等在“涡动力学”一书中就定义涡是“涡量集中区”，又在中国科学发表的文章（2018）中明确定义“涡就是涡量管（Vorticity Tube）周围被无旋流包围”。但是赫氏理论明显地碰到无可置疑的矛盾。比如层流渠道流的管壁附近涡量很大，但并没有看到任何流体转动或者旋涡。人类开始认识到涡量不代表旋转，是流体转动和剪切的混合物。在过去的四十年多里，人类开发了许多涡识别判据，比如Q-，Lambda2, Lambda-Ci,等等，我们称之为涡的第二代定义，但它们都是标量。涡是矢量有方向有旋转轴，人类的常识是矢量不能用一个标量定义。第二代需要阈值来描述涡结构，但阈值是任意的和经验的，不同的阈值会给出完全不同的涡结构。不仅如此，它们都受到不同程度剪切污染，不能准确给出涡的旋转强度和旋转周期。直到2018年UTA刘超群团队给出Liutex，也就是涡的第三代定义，其方向是速度梯度矩阵的特征向量，其大小是流体旋转角速度的二倍，人类有史以来才第一次找到涡的准确数学定义，只有Liutex才能给出涡的转轴和精确角速度，自然界的漩涡涡核就是Liutex的极值线或者Liutex线集中区域（不是涡量集中区域）。 湍流里面全是涡，没有涡定义怎么定量研究湍流？这就打开了涡和湍流研究的一扇大门，开辟了涡和湍流定量研究的新纪元。由于涡无处不在，可以预期Liutex会对全球与流体有关的上百个科学研究领域和数万个研究工作者产生巨大影响。JHD周主编提出判别涡的六大准则，第一代第二代所有方法几乎无法回答这六大准则提出的问题，只有第三代也就是Liutex理论能成功地回答所有问题。这一里程碑式的突破已经为各国许多研究领域的学者所证实，包括许多中国学者和欧美科学家。欧美十个国家十五名空间科学家最近在著名的空间科学杂志上发表评论文章，以无可争辩的事实显示只有Liutex才能给出准确的涡强度和涡转动周期。但是这里就有一个令人困惑的问题，那就是为什么人类要用一百六十多年的时间才发现Liutex，也就是为什么要花一百六十多年的时间才给出涡的数学定义？本文给出了合理的回答，原来人们错误地认为是速度梯度，其实不是，速度梯度是。速度梯度矩阵的特征向量就是转轴或者Liutex的方向。是速度梯度的转置，和速度梯度有共同的特征值，但特征向量完全不同，但是人们习惯了用代表速度梯度，这也就是各国学者长期找不到涡数学定义Liutex的主要原因之一。除此之外，刘超群和俞一飞在此文中还仔细推导了坐标轴的Q-旋转和P-旋转的方法和具体公式，速度梯度张量的主分解，尤其是第一次给出速度梯度的散度公式，，这一公式不仅具有极其重要的理论意义，而且为推导新的流体动力学控制方程和Liutex动力学奠定了基石。

主要结论

  1. 二阶张量/矢量一般可以用矩阵表示，但它们是完全不同的概念，前者是唯一的，后者有无数，取决于坐标选择。
  2. 矩阵有加减乘求逆转置，张量/矢量只有点积叉积并矢，二者不是完全等价，我们不能随便丢弃点积符号和并矢符号
  3. 由于，但，
    所以速度梯度定义是许多书搞错了。
  1. 速度梯度的主张量和主分解是：
    也就是转动拉伸和剪切
  1. 为了得到速度梯度张量的主张量，我们需要Q-旋转和P-旋转，本文提供了Q-旋转和P-旋转的详细推导，见方程（43）和（46）
  2. Liutex方向是的特征向量，不是的特征向量，这也许是为什么人类要花一百六十年才找到Liutex（也就是涡精确的数学定义）的主要原因之一。Liutex大小见方程（35）
  3. 本文给出速度梯度张量的散度方程（64），定理2 对我们进一步根据Liutex的新的流体运动学去推导流体力学控制方程有极大的指导意义。

作者简介

刘超群从清华大学力学系于1968年学士毕业和1981年硕士毕业，1989年在美国科罗拉多大学丹佛分校获得应用数学博士，现在是美国德州大学阿灵顿分校（UTA）杰出终身教授和数值模拟和建模中心主任。他从事流体力学研究，用高阶数值格式做流动转捩和湍流的直接数值模拟（DNS）已经三十多年，出版了十四本书，141篇期刊论文和171篇会议论文，拿到51项研究课题。他是UTA团队的领头人。他是Liutex和第三代涡识别方法的创始人和主要贡献者，包括以Liutex为基础各种识别方法，涡量的RS分解，速度梯度张量的UTA R-NR 分解和转动-拉伸-剪切的主分解。他也是基于Liutex的新流体运动学的创始人。

俞一飞从2018年于南京航空航天大学工程力学专业本科毕业，现于德州大学阿灵顿分校攻读博士，师从刘超群教授。主要从事涡识别，流动稳定性，objective vortex等方面的研究。已发表期刊论文、会议论文十余篇。